
OPENING QUESTIONS: Here's an interesting tidbit... a "neutrino" is a subatomic particle with a very tiny amount of mass. It wasn't actually detected for twenty or so years after it was incorporated into modern physics.
Background:Certain radioactive elements have unstable nuclei. Inside the neutrons in those nuclei a 'down' quark spontaneously changes into an 'up' quark which turns the neutron into a proton in a process known as beta decay and is governed by the 'weak force'. In that process an electron is spontaneous ejected (changing the charge from 0 to +1 requires that) along with an electron neutrino.
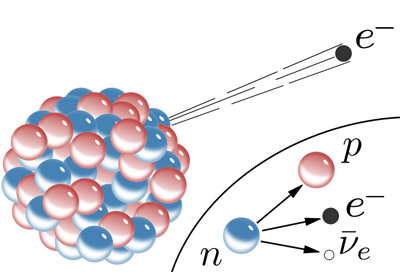
So... if it wasn't even detected, why was it incorporated into modern physics?
OBJECTIVE: I will be able to show the direction of the cross product of two unit vectors during today's class
FORMULAE OBJECTUS:
L = r x p = Iω (L, r, p and ω are ALL vectors)
∑τ = dL/dt (This is the another form of Newton's 2nd... if we add up all the torques acting on an object, any NET torque will cause the angular momentum of the object to change.
WORDS FOR TODAY:
cross product - multiplying vectors
right hand rule: "If you grip the imaginary axis of rotation of the rotational force so that your fingers point in the direction of the force, then the extended thumb points in the direction of the torque vector." from the website: https://web.ua.es/docivis/magnet/righthand_rule.html
Linear Momentum (L) units: kgm2/s
WORK O' THE DAY:
A coupla units back we learned about the 'dot' product and how that helps us for situations such as work, when we are concerned about the component of force in the direction of an object's motion.
Now let's learn CROSS PRODUCT
We know from our previous unit that torque = r x F (where are is the length of the 'lever arm' and F is the amount of force applied.
However...
That's kinda of the jv version of torque.... now we're going to step up a bit to 3 dimensional torque. Afterall, the displacement in which a torque is applied is a vector, and as such it can exist in three dimensions.... ditto with force.
Let's take a departure from the text for a moment (since it takes a much more mathematical approach). We will come at this again in E & M so might as well go to it now!
To wit:
Recall the i, j & k unit vectors... are... WHAT? again?
Now hold out your hand so that your fingers are pointing in the positive x direction... Now please 'curl' your fingers in the positive y direction. Now please check out the direction your thumb is pointing?
Congrats... you just 'curled' i x j to get k.
Try it again, this time try 'curling' in the k x -j direction...
point your fingers sso they are in the positive k direction and curl them in the minus j direction to get i
let's check the opposite to make sure we're doing it right. -k x -j should equal the opposite (-i). Let try: Point your fingers in negative k direction and curl them in the direction of negative j.... et voila! it is indeed -i
Notice that it just ain't possible to curl i x i or i x -1... which means... what?
Let's practice... be sure and keep this orientation in mind. Let's make our "standard" orientation +x, +y, +z. In that instance, the fingers in your right hand will be pointing to the right (+x), your thumb will be point straight up (+y) and the back of your hand will be pointing in +z.
If you like matrices... matrixes....matri-somethings, try this (of course *you* have to fill in the blanks, 'cause I'm not gonna):
Add 'em up:
ANSWER:
I'm not quite sure why the book doesn't do that, it's a rather helpful skill to have.
Now please work through examples 11.1 and 11.2
What happens when you hit the brakes on you (non-Prius-type) car?
How is that different from when you hit the brakes on a Prius-type car?
Coursework:
11.11, 12, 18 beginning on page 355